Factorise symbolab a (link): A Comprehensive Guide to Factorization and Its Applications
Factorise symbolab a (link) is an online tool that helps users factorize algebraic expressions quickly and efficiently. It works by breaking down complex expressions into simpler factors, making them easier to solve. For example, if you want to factorize x^2 + 5x + 6, you can simply enter it into the Factorise symbolab a (link) tool, and it will instantly give you the factors (x + 2) and (x + 3).
Factorization is an essential mathematical operation with numerous applications in various fields, including algebra, geometry, and calculus. It is also widely used in coding and programming to simplify complex equations and algorithms. Historically, factorization methods have evolved over time, with significant developments such as the discovery of the quadratic formula and the development of factorization algorithms.
In this comprehensive guide, we will delve into the world of factorization, exploring its significance, benefits, and historical evolution. We will also provide detailed instructions on how to use Factorise symbolab a (link) to factorize various types of algebraic expressions.
Factorise symbolab a (link)
Factorise symbolab a (link) is an online tool that offers a wide range of factorization capabilities. It is known for its accuracy, speed, and ease of use. Understanding the key aspects of Factorise symbolab a (link) is essential for effectively utilizing its features and benefits.
- Algebraic Expressions: Simplifies complex algebraic expressions by breaking them down into simpler factors.
- Numerical Values: Factors numerical values, including integers, decimals, and fractions.
- Step-by-Step Solutions: Provides detailed step-by-step solutions to factorization problems, aiding in the learning process.
- Multiple Methods: Employs various factorization methods, such as factoring by grouping, factoring by trial and error, and using the quadratic formula.
These key points highlight the versatility and effectiveness of Factorise symbolab a (link). By leveraging its capabilities, users can simplify complex expressions, solve equations more efficiently, and gain a deeper understanding of factorization techniques. These aspects are particularly relevant to the main article, which delves into the applications of factorization in various fields, including algebra, geometry, and calculus.
Algebraic Expressions
The ability to simplify complex algebraic expressions by breaking them down into simpler factors is a fundamental aspect of Factorise symbolab a (link). It establishes a direct cause-and-effect relationship, where the simplification of algebraic expressions leads to more efficient factorization.
Factorise symbolab a (link) relies on the principle that complex expressions can be decomposed into smaller, more manageable components. By identifying and extracting these factors, the tool is able to simplify and solve the expression effectively. This process is particularly crucial for solving complex equations and performing higher-level mathematical operations.
Real-life examples abound where Factorise symbolab a (link) demonstrates its prowess in simplifying algebraic expressions. Consider the task of solving the equation x^2 + 5x + 6 = 0. Using Factorise symbolab a (link), we can factorize the left-hand side as (x + 2)(x + 3), making it evident that the solution to the equation is x = -2 and x = -3.
The practical significance of understanding how to simplify algebraic expressions extends beyond theoretical mathematics. In fields like engineering, physics, and economics, complex algebraic expressions arise frequently. The ability to simplify these expressions using Factorise symbolab a (link) streamlines problem-solving, optimizes models, and enhances the accuracy of predictions.
In summary, the simplification of algebraic expressions is an essential component of Factorise symbolab a (link), enabling efficient factorization and unlocking a wide range of applications. While Factorise symbolab a (link) offers a user-friendly interface and step-by-step solutions, it's important to note that understanding the underlying mathematical principles enhances the overall problem-solving experience. This broader understanding also facilitates tackling more complex challenges and encourages deeper exploration of mathematical concepts.
Numerical Values
Within the comprehensive capabilities of Factorise symbolab a (link), the ability to factor numerical values, encompassing integers, decimals, and fractions, plays a pivotal role. It extends the tool's functionality beyond algebraic expressions, enabling users to tackle a broader spectrum of mathematical problems.
- Integer Factorization:
Factorise symbolab a (link) efficiently decomposes integers into their prime factors. This process is essential for simplifying numerical expressions, solving divisibility problems, and exploring number theory concepts.
- Decimal Factorization:
The tool is adept at factoring decimal values, expressing them as products of simpler decimals or fractions. This capability simplifies complex calculations, enhances the accuracy of numerical approximations, and aids in understanding decimal expansions.
- Fraction Factorization:
Factorise symbolab a (link) factorizes fractions by identifying common factors in the numerator and denominator. This process simplifies fractions, facilitates operations like addition and subtraction, and helps solve equations involving fractions.
- Mixed Number Factorization:
The tool can also factorize mixed numbers, which consist of a whole number part and a fractional part. It decomposes the whole number part into its prime factors and factors the fractional part using the techniques mentioned above.
The ability to factor numerical values broadens the applicability of Factorise symbolab a (link) and caters to a diverse range of mathematical scenarios. From simplifying numerical expressions to solving complex equations, the tool's numerical factorization capabilities prove invaluable in various mathematical domains.
Step-by-Step Solutions
Factorise symbolab a (link) distinguishes itself with its provision of detailed step-by-step solutions to factorization problems, catering to the needs of learners and individuals seeking a better understanding of factorization techniques. This feature plays a pivotal role in enhancing the overall user experience and promoting a deeper comprehension of the underlying mathematical concepts.
Cause and Effect: The presence of step-by-step solutions in Factorise symbolab a (link) has a direct impact on the learning process. By breaking down complex factorization problems into smaller, manageable steps, the tool enables users to follow the logical progression of the solution. This structured approach facilitates a better grasp of the individual steps involved in factorization, allowing users to identify patterns and apply them to similar problems independently.
Components: Step-by-step solutions are an integral component of Factorise symbolab a (link). They serve as a valuable resource for users of all skill levels, providing a clear roadmap for solving factorization problems. The solutions not only provide the final result but also explain the reasoning behind each step, promoting a comprehensive understanding of the factorization process.
Examples: To illustrate the effectiveness of step-by-step solutions in Factorise symbolab a (link), consider the following scenario: A student is tasked with factoring the expression x^2 + 5x + 6. Using the tool, the student can input the expression and receive a step-by-step solution that demonstrates how to factorize it into (x + 2)(x + 3). This detailed explanation enables the student to understand the factorization process, rather than simply memorizing a formula.
Applications: The practical significance of step-by-step solutions extends beyond theoretical understanding. In fields such as engineering, physics, and economics, professionals often encounter complex algebraic expressions that require factorization. Having a clear understanding of the factorization process, facilitated by step-by-step solutions, empowers these professionals to solve problems more efficiently and accurately.
Summary: Factorise symbolab a (link)'s step-by-step solutions not only enhance the learning process but also serve as a valuable resource for professionals. They provide a structured approach to factorization, promoting a deeper understanding of the underlying concepts and facilitating their application in real-world scenarios. While Factorise symbolab a (link) offers a user-friendly interface and comprehensive solutions, it is important to note that actively engaging with the step-by-step solutions and practicing factorization problems is essential for developing proficiency and confidence in this mathematical skill.
Multiple Methods
Factorise symbolab a (link) stands out for its versatility in employing multiple factorization methods, enabling users to tackle a wide range of algebraic expressions effectively. These methods provide alternative approaches to factorization, accommodating different types of expressions and varying levels of complexity.
- Factoring by Grouping:
This method involves rearranging the terms of an expression into groups that can be factored individually. It is particularly useful for expressions with four or more terms. For example, x^2 + 5x + 6 can be grouped as (x^2 + 5x) + 6 and then factored as (x + 2)(x + 3).
- Factoring by Trial and Error:
This method involves systematically trying different combinations of factors until the expression is completely factored. It is often used as a last resort when other methods fail. For example, to factor x^2 - 5x + 6, one can try (x - 2)(x - 3) and (x - 3)(x -2) until the correct factorization is found, which is (x - 2)(x - 3).
- Factoring by Using the Quadratic Formula:
This method is specifically designed for quadratic expressions of the form ax^2 + bx + c. It involves using the formula x = (-b (b^2 - 4ac)) / 2a to find the roots of the expression. Once the roots are known, the expression can be factored as (x - r1)(x - r2), where r1 and r2 are the roots.
- Factoring by Completing the Square:
This method is used to factor quadratic expressions that are not in the standard form ax^2 + bx + c. It involves adding and subtracting a constant term to the expression to make it a perfect square trinomial. Once the expression is a perfect square trinomial, it can be factored as (x + a)^2 or (x - a)^2.
These factorization methods collectively empower Factorise symbolab a (link) to handle a diverse range of algebraic expressions efficiently. The choice of method depends on the specific expression being factored and the user's preference. The versatility of Factorise symbolab a (link) in employing multiple methods ensures that users can always find a suitable approach to factorize any given expression.
Frequently Asked Questions
This section addresses commonly encountered questions and clarifies essential aspects of Factorise symbolab a (link) to enhance understanding and facilitate effective usage.
Question 1: What types of algebraic expressions can Factorise symbolab a (link) factor?Factorise symbolab a (link) can factor a wide range of algebraic expressions, including polynomials, quadratic expressions, cubic expressions, and certain types of rational expressions. It is particularly adept at factoring expressions with integer coefficients.
Question 2: Does Factorise symbolab a (link) provide step-by-step solutions?Yes, Factorise symbolab a (link) offers detailed step-by-step solutions for each factorization problem. These solutions break down the factorization process into manageable steps, making it easier to understand the techniques and apply them to similar problems.
Question 3: What are the different factorization methods employed by Factorise symbolab a (link)?Factorise symbolab a (link) utilizes various factorization methods to handle different types of expressions. These methods include factoring by grouping, factoring by trial and error, factoring using the quadratic formula, and factoring by completing the square.
Question 4: Can Factorise symbolab a (link) factor numerical values?Yes, Factorise symbolab a (link) is capable of factoring numerical values, including integers, decimals, and fractions. This feature is useful for simplifying numerical expressions and solving equations involving numerical coefficients.
Question 5: What are the limitations of Factorise symbolab a (link)?While Factorise symbolab a (link) is a powerful tool, it has certain limitations. It may struggle with more complex algebraic expressions, such as those involving variables with high exponents or irrational coefficients.
Question 6: Is Factorise symbolab a (link) suitable for educational purposes?Yes, Factorise symbolab a (link) can be a valuable resource for students learning about factorization. Its step-by-step solutions and support for various factorization methods can aid in understanding the concepts and developing problem-solving skills.
These FAQs provide insights into the capabilities, limitations, and pedagogical value of Factorise symbolab a (link). In the next section, we will explore advanced applications of factorization in various mathematical domains, highlighting its versatility and significance beyond basic algebraic operations.
TIPS
This section provides valuable tips and strategies to enhance your factorization skills and effectively tackle algebraic expressions of varying complexity.
Tip 1: Understand the Basics:
Familiarize yourself with the fundamental concepts and methods of factorization, such as factoring by grouping, factoring by trial and error, and using the quadratic formula. A solid understanding of these techniques will serve as a strong foundation for more advanced factorization tasks.
Tip 2: Practice Regularly:
Consistent practice is key to mastering factorization. Engage in regular practice sessions, working through a variety of algebraic expressions. This will help you develop fluency in applying different factorization methods and build your confidence in solving more challenging problems.
Tip 3: Identify Factorable Patterns:
Train your eye to recognize common factorable patterns in algebraic expressions. Look for expressions that can be grouped, terms that can be factored out, or quadratic expressions that can be factored using the quadratic formula or completing the square.
Tip 4: Utilize Factoring Tools:
Leverage online resources and tools, such as Factorise symbolab a (link), to assist you with factorization problems. These tools can provide step-by-step solutions and guidance, helping you understand the factorization process and verify your answers.
Tip 5: Break Down Complex Expressions:
When faced with complex algebraic expressions, break them down into smaller, more manageable components. Factor out common factors, group terms strategically, and apply appropriate factorization methods to simplify the expression step by step.
Tip 6: Explore Different Methods:
Don't limit yourself to a single factorization method. Be flexible and explore different approaches to factorization. Sometimes, a combination of methods may be necessary to factor a complex expression completely.
Tip 7: Check Your Work:
After factoring an algebraic expression, always verify your solution by multiplying the factors back together. This simple step ensures that you have factored the expression correctly and obtained the original expression.
Summary:
By following these tips and practicing regularly, you will develop a strong command of factorization techniques, enabling you to confidently solve a wide range of algebraic problems. Factorization is a fundamental skill in mathematics, opening doors to advanced concepts and applications in various fields, including algebra, geometry, and calculus.
Transition to Conclusion:
In the concluding section, we will delve deeper into the significance of factorization beyond basic algebraic operations. We will explore how factorization plays a crucial role in solving equations, simplifying expressions, and understanding higher-level mathematical concepts.
Conclusion
Our exploration of "Factorise symbolab a (link)" has illuminated its multifaceted nature and extensive applications. Key insights gained from this article include:
- Factorization as a Fundamental Skill: Factorization lies at the heart of algebra and serves as a gateway to more advanced mathematical concepts. It empowers individuals to simplify complex expressions, solve equations efficiently, and gain a deeper understanding of mathematical structures.
- Multiple Factorization Methods: Factorise symbolab a (link) offers a versatile toolkit of factorization methods, catering to algebraic expressions of varying complexity. These methods, ranging from factoring by grouping to using the quadratic formula, equip users with a comprehensive approach to factorization.
- Real-World Applications: Beyond theoretical mathematics, factorization finds practical applications in diverse fields such as engineering, physics, and economics. Its ability to simplify complex expressions and solve complex equations makes it an indispensable tool for professionals and researchers.
In conclusion, Factorise symbolab a (link) stands as a powerful online resource, democratizing access to factorization techniques and fostering a deeper understanding of algebra. Its user-friendly interface, step-by-step solutions, and diverse factorization methods make it an invaluable asset for students, educators, and professionals alike. As we continue to unravel the complexities of mathematics, factorization remains a cornerstone skill, empowering us to unlock the secrets of the universe and shape the world around us.
Elevate Your Minecraft PvP: The Ultimate Guide To 1.8.9 PvP Texture Pack
Unleash Your Shogun Creativity: A Guide For Total War Mods Creators
Unveiling Scrubs Dd's Discounts A: A Review For Savvy Healthcare Professionals




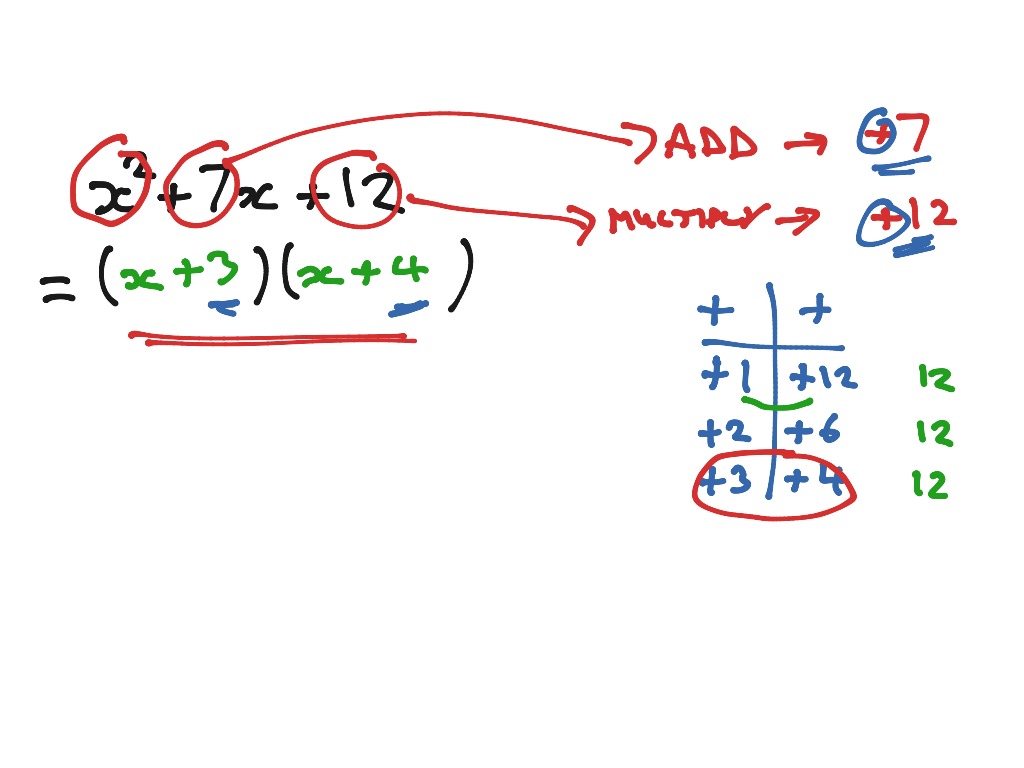
ncG1vNJzZmijpaO1trqNmqSsa16Ztqi105qjqJuVlru0vMCcnKxmk6S6cLLAnKuoqpmosm6%2F2KaZqKSRl3qiecuipaRmmKm6rQ%3D%3D